Force control of task-space orientation

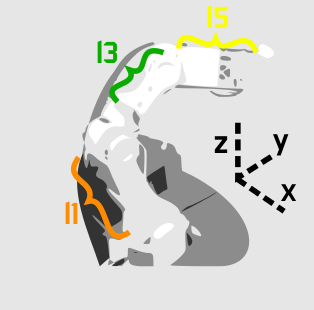
So you want to use force control to control the orientation of your end-effector, eh? What a noble endeavour. I, too, wished to control the orientation of the end-effector. While the journey was long and arduous, the resulting code is short and quick to implement. All of the code for reproducing the results shown here is up on my GitHub and in the ABR Control repo. 

Introduction

There are numerous resources that introduce the topic of orientation control, so I’m not going to do a full rehash here. I will link to resources that I found helpful, but a quick google search will pull up many useful references on the basics. 

When describing the orientation of the end-effector there are three different primary methods used: Euler angles, rotation matrices, and quaternions. The Euler angles , and denote roll, pitch, and yaw, respectively. Rotation matrices specify 3 orthogonal unit vectors, and I describe in detail how to calculate them in this post on forward transforms. And quaternions are 4-dimensional vectors used to describe 3 dimensional orientation, which provide stability and require less memory and compute but are more complicated to understand.

Most modern robotics control is done using quaternions because they do not have singularities, and it is straight forward to convert them to other representations. Fun fact: Quaternion trajectories also interpolate nicely, where Euler angles and rotation matrices do not, so they are used in computer graphics to generate a trajectory for an object to follow in orientation space.

While you won’t need a full understanding of quaternions to use the orientation control code, it definitely helps if anything goes wrong. If you are looking to learn about or brush up on quaternions, or even if you’re not but you haven’t seen this resource, you should definitely check out these interactive videos by Grant Sanderson and Ben Eater. They have done an incredible job developing modules to give people an intuition into how quaternions work, and I can’t recommend their work enough. There’s also a non-interactive video version that covers the same material.

In control literature, angular velocity and acceleration are denoted and . It’s important to remember that is denoting a velocity, and not a position, as we work through things or it could take you a lot longer to understand than it otherwise might…

How to generate task-space angular forces

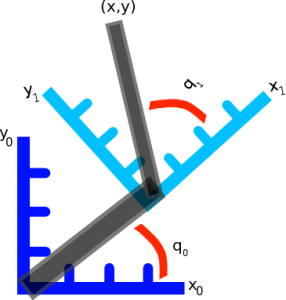
So, if you recall a post long ago on Jacobians, our task-space Jacobian has 6 rows:

In position control, where we’re only concerned about the position of the hand, the angular velocity dimensions are stripped out of the Jacobian so that it’s a 3 x n_joints matrix rather than a 6 x n_joints matrix. So the orientation of the end-effector is not controlled at all. When we did this, we didn’t need to worry or know anything about the form of the angular velocities.

Now that we’re interested in orientation control, however, we will need to learn up (and thank you to Yitao Ding for clarifying this point in comments on the original version of this post). The Jacobian for the orientation describes the rotational velocities around each axis with respect to joint velocities. The rotational velocity of each axis “happens” at the same time. It’s important to note that this is not the same thing as Euler angles, which are applied sequentially.

To generate our task-space angular forces we will have to generate an orientation angle error signal of the appropriate form. To do that, first we’re going to have to get and be able to manipulate the orientation representation of the end-effector and our target.

Transforming orientation between representations

We can get the current end-effector orientation in rotation matrix form quickly, using the transformation matrices for the robot. To get the target end-effector orientation in the examples below we’ll use the VREP remote API, which returns Euler angles.

It’s important to note that Euler angles can come in 12 different formats. You have to know what kind of Euler angles you’re dealing with (e.g. rotate around X then Y then Z, or rotate around X then Y then X, etc) for all of this to work properly. It should be well documented somewhere, for example the VREP API page tells us that it will return angles corresponding to x, y, and then z rotations.

The axes of rotation can be static (extrinsic rotations) or rotating (intrinsic rotations). NOTE: The VREP page says that they rotate around an absolute frame of reference, which I take to mean static, but I believe that’s a typo on their page. If you calculate the orientation of the end-effector of the UR5 using transform matrices, and then convert it to Euler angles with axes='rxyz' you get a match with the displayed Euler angles, but not with axes='sxyz'.

Now we’re going to have to be able to transform between Euler angles, rotation matrices, and quaternions. There are well established methods for doing this, and a bunch of people have coded things up to do it efficiently. Here I use the very handy transformations module from Christoph Gohlke at the University of California. Importantly, when converting to quaternions, don’t forget to normalize the quaternions to unit length.

from abr_control.arms import ur5 as arm
from abr_control.interfaces import VREP
from abr_control.utils import transformations

robot_config = arm.Config()
interface = VREP(robot_config)
interface.connect()

feedback = interface.get_feedback()
# get the end-effector orientation matrix
R_e = robot_config.R('EE', q=feedback['q'])
# calculate the end-effector unit quaternion
q_e = transformations.unit_vector(
    transformations.quaternion_from_matrix(R_e))

# get the target information from VREP
target = np.hstack([
    interface.get_xyz('target'),
    interface.get_orientation('target')])
# calculate the target orientation rotation matrix
R_d = transformations.euler_matrix(
    target[3], target[4], target[5], axes='rxyz')[:3, :3]
# calculate the target orientation unit quaternion
q_d = transformations.unit_vector(
    transformations.quaternion_from_euler(
        target[3], target[4], target[5],
        axes='rxyz'))  # converting angles from 'rotating xyz'

Generating the orientation error

I implemented 4 different methods for calculating the orientation error, from (Caccavale et al, 1998), (Yuan, 1988) and (Nakinishi et al, 2008), and then one based off some code I found on Stack Overflow. I’ll describe each below, and then we’ll look at the results of applying them in VREP.

Method 1 – Based on code from StackOverflow

Given two orientation quaternion and , we want to calculate the rotation quaternion that takes us from  to :

To isolate , we right multiply by the inverse of . All orientation quaternions are of unit length, and for unit quaternions the inverse is the same as the conjugate. To calculate the conjugate of a quaternion, denoted here, we negate either the scalar or vector part of the quaternion, but not both.

Great! Now we know how to calculate the rotation needed to get from the current orientation to the target orientation. Next, we have to get from a set of target Euler angle forces. In A new method for performing digital control system attitude computations using quaternions (Ickes, 1968), he mentions mention that

For control purposes, the last three elements of the quaternion define the roll, pitch, and yaw rotational errors…

So you can just take the vector part of the quaternion and use that as your desired Euler angle forces.

# calculate the rotation between current and target orientations
q_r = transformations.quaternion_multiply(
    q_target, transformations.quaternion_conjugate(q_e))

# convert rotation quaternion to Euler angle forces
u_task[3:] = ko * q_r[1:] * np.sign(q_r[0])

NOTE: You will run into issues when the angle is crossed where the arm ‘goes the long way around’. To account for this, use q_r[1:] * np.sign(q_r[0]). This will make sure that you always rotate along a trajectory < 180 degrees towards the target angle. The reason that this crops up is because there are multiple different quaternions that can represent the same orientation.

The following figure shows the arm being directed from and to the same orientations, where the one on the left takes the long way around, and the one on the right multiplies by the sign of the scalar component of the quaternion as specified above.

• 

• 

---

Method 2 – Quaternion feedback from Resolved-acceleration control of robot manipulators: A critical review with experiments (Caccavale et al, 1998)

In section IV, equation (34) of this paper they specify the orientation error to be calculated as

where is the rotation matrix for the end-effector, and is the vector part of the unit quaternion that can be extracted from the rotation matrix

.

To implement this is pretty straight forward using the transforms.py module to handle the representation conversions:

# From (Caccavale et al, 1997)
# Section IV - Quaternion feedback
R_ed = np.dot(R_e.T, R_d)  # eq 24
q_ed = transformations.quaternion_from_matrix(R_ed)
q_ed = transformations.unit_vector(q_ed)
u_task[3:] = -np.dot(R_e, q_ed[1:])  # eq 34

---

Method 3 – Angle/axis feedback from Resolved-acceleration control of robot manipulators: A critical review with experiments (Caccavale et al, 1998)

In section V of the paper, they present an angle / axis feedback algorithm, which overcomes the singularity issues that classic Euler angle methods suffer from. The algorithm defines the orientation error in equation (45) to be calculated

,

where and are the scalar and vector part of the quaternion representation of 

Where is the rotation matrix representing the desired orientation and is the rotation matrix representing the end-effector orientation. The code implementation for this looks like:

# From (Caccavale et al, 1997)
# Section V - Angle/axis feedback
R_de = np.dot(R_d, R_e.T)  # eq 44
q_ed = transformations.quaternion_from_matrix(R_de)
q_ed = transformations.unit_vector(q_ed)
u_task[3:] = -2 * q_ed[0] * q_ed[1:]  # eq 45

From playing around with this briefly, it seems like this method also works. The authors note in the discussion that it may “suffer in the case of large orientation errors”, but I wasn’t able to elicit poor behaviour when playing around with it in VREP. The other downside they mention is that the computational burden is heavier with this method than with quaternion feedback.

---

Method 4 – From Closed-loop manipulater control using quaternion feedback (Yuan, 1988) and Operational space control: A theoretical and empirical comparison (Nakanishi et al, 2008)

This was the one method that I wasn’t able to get implemented / working properly. Originally presented in (Yuan, 1988), and then modified for representing the angular velocity in world and not local coordinates in (Nakanishi et al, 2008), the equation for generating error (Nakanishi eq 72):

where and are the scalar and vector components of the quaternions representing the end-effector and target orientations, respectively, and is defined in (Nakanishi eq 73):

My code for this implementation looks like:

S = np.array([
    [0.0, -q_d[2], q_d[1]],
    [q_d[2], 0.0, -q_d[0]],
    [-q_d[1], q_d[0], 0.0]])

u_task[3:] = -(q_d[0] * q_e[1:] - q_e[0] * q_d[1:] +
               np.dot(S, q_e[1:]))

If you understand why this isn’t working, if you can provide a working code example in the comments I would be very grateful.

---

Generating the full orientation control signal

The above steps generate the task-space control signal, and from here I’m just using standard operational space control methods to take u_task and transform it into joint torques to send out to the arm. With possibly the caveat that I’m accounting for velocity in joint-space, not task space. Generating the full control signal looks like:

 
# which dim to control of [x, y, z, alpha, beta, gamma]
ctrlr_dof = np.array([False, False, False, True, True, True])

feedback = interface.get_feedback()
# get the end-effector orientation matrix
R_e = robot_config.R('EE', q=feedback['q'])
# calculate the end-effector unit quaternion
q_e = transformations.unit_vector(
    transformations.quaternion_from_matrix(R_e))

# get the target information from VREP
target = np.hstack([
    interface.get_xyz('target'),
    interface.get_orientation('target')])
# calculate the target orientation rotation matrix
R_d = transformations.euler_matrix(
    target[3], target[4], target[5], axes='rxyz')[:3, :3]
# calculate the target orientation unit quaternion
q_d = transformations.unit_vector(
    transformations.quaternion_from_euler(
        target[3], target[4], target[5],
        axes='rxyz'))  # converting angles from 'rotating xyz'

# calculate the Jacobian for the end effectora
# and isolate relevate dimensions
J = robot_config.J('EE', q=feedback['q'])[ctrlr_dof]

# calculate the inertia matrix in task space
M = robot_config.M(q=feedback['q'])

# calculate the inertia matrix in task space
M_inv = np.linalg.inv(M)
Mx_inv = np.dot(J, np.dot(M_inv, J.T))
if np.linalg.det(Mx_inv) != 0:
    # do the linalg inverse if matrix is non-singular
    # because it's faster and more accurate
    Mx = np.linalg.inv(Mx_inv)
else:
    # using the rcond to set singular values < thresh to 0
    # singular values < (rcond * max(singular_values)) set to 0
    Mx = np.linalg.pinv(Mx_inv, rcond=.005)

u_task = np.zeros(6)  # [x, y, z, alpha, beta, gamma]

# generate orientation error
# CODE FROM ONE OF ABOVE METHODS HERE

# remove uncontrolled dimensions from u_task
u_task = u_task[ctrlr_dof]

# transform from operational space to torques and
# add in velocity and gravity compensation in joint space
u = (np.dot(J.T, np.dot(Mx, u_task)) -
     kv * np.dot(M, feedback['dq']) -
     robot_config.g(q=feedback['q']))

# apply the control signal, step the sim forward
interface.send_forces(u)

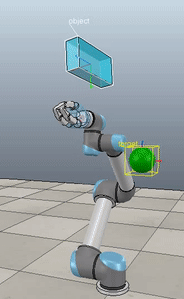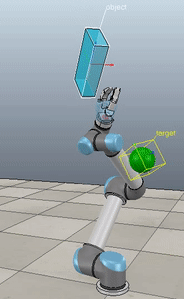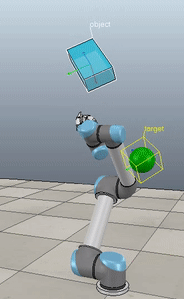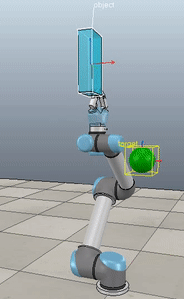
The control script in full context is available up on my GitHub along with the corresponding VREP scene. If you download and run both (and have the ABR Control repo installed), then you can generate fun videos like the following:

• 

  Method 1 – Stack overflow code

• 

  Method 2 – Caccavale quaternion

• 

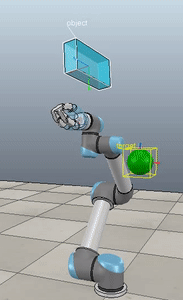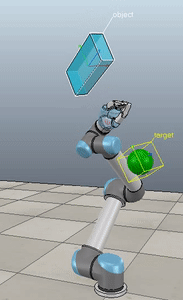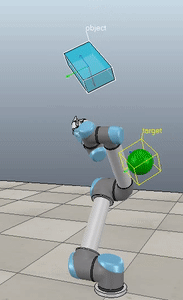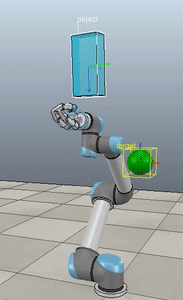
  Method 3 – Caccavale angle/axis

• 

  Method 4 – Yuan / Nakanishi

Here, the green ball is the target, and the end-effector is being controlled to match the orientation of the ball. The blue box is just a visualization aid for displaying the orientation of the end-effector. And that hand is on there just from another project I was working on then forgot to remove but already made the videos so here we are. It’s set to not affect the dynamics so don’t worry. The target changes orientation once a second. The orientation gain for these trials is ko=200 and kv=np.sqrt(600).

The first three methods all perform relatively similarly to each other, although method 3 seems to be a bit faster to converge to the target orientation after the first movement. But it’s pretty clear something is terribly wrong with the implementation of the Yuan algorithm in method 4; brownie points for whoever figures out what!

Controlling position and orientation

So you want to use force control to control both position and orientation, eh? You are truly reaching for the stars, and I applaud you. For the most part, this is pretty straight-forward. But there are a couple of gotchyas so I’ll explicitly go through the process here.

How many degrees-of-freedom (DOF) can be controlled?

If you recall from my article on Jacobians, there was a section on analysing the Jacobian. It comes down to two main points: 1) The Jacobian specifies which task-space DOF can be controlled. If there is a row of zeros, for example, the corresponding task-space DOF (i.e. cannot be controlled. 2) The rank of the Jacobian determines how many DOF can be controlled at the same time.

For example, in a two joint planar arm, the variables can be controlled, but cannot be controlled because their corresponding rows are all zeros. So 3 variables can potentially be controlled, but because the Jacobian is rank 2 only two variables can be controlled at a time. If you try to control more than 2 DOF at a time things are going to go poorly. Here are some animations of trying to control 3 DOF vs 2 DOF in a 2 joint arm:

• 

  controlling 3 DOF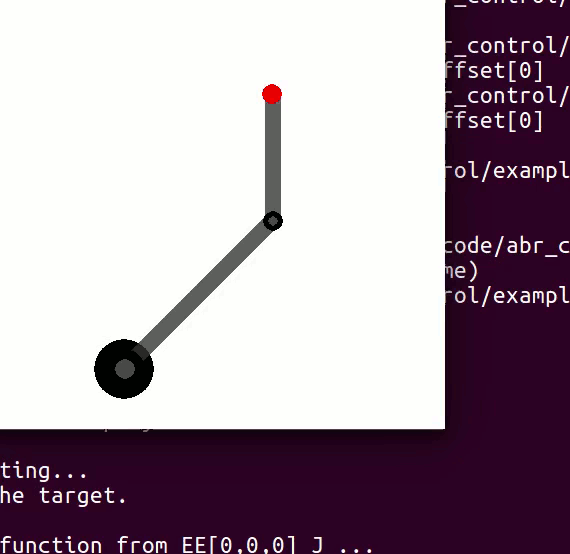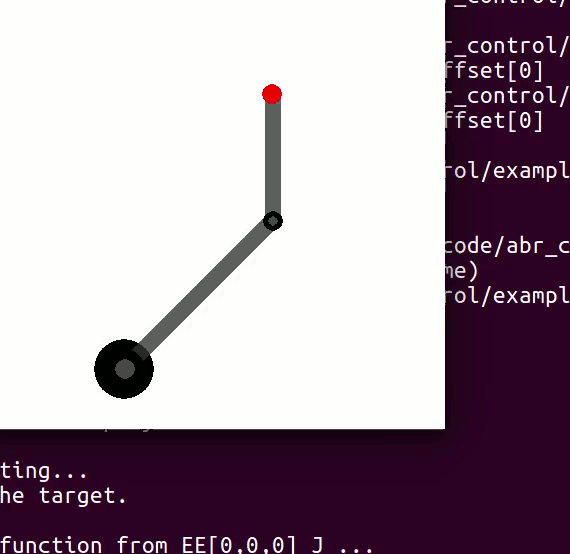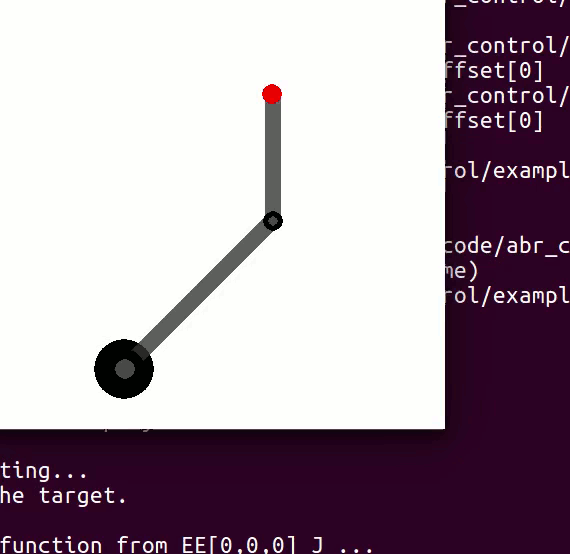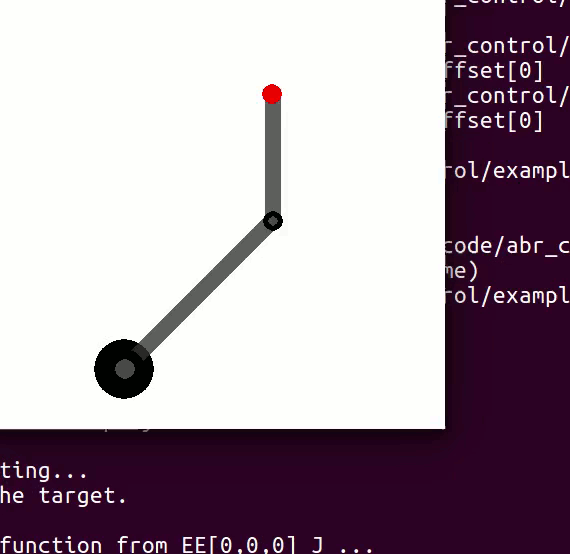

• 

  controlling 2 DOF

How to specify which DOF are being controlled?

Okay, so we don’t want to try to control too many DOF at once. Got it. Let’s say we know that our arm has 3 DOF, how do we choose which DOF to control? Simple: You remove the rows from you Jacobian and your control signal that correspond to task-space DOF you don’t want to control.

To implement this in code in a flexible way, I’ve chosen to specify an array with 6 boolean elements, set to True if you want to control the corresponding task space parameter and False if you don’t. For example, if you to control just the parameters, you would set ctrl_dof = [True, True, True, False, False, False].

We then strip the Jacobian and task space control signal down to the relevant rows with J = robot_config.('EE', q)[ctrlr_dof] and u_task = (current - target)[ctrlr_dof]. This means that both current and target must be 6-dimensional vectors specifying the current and target values, respectively, regardless of how many dimensions we’re actually controlling.

Generating a position + orientation control signal

The UR5 has 6 degrees of freedom, so we’re able to fully control the task space position and orientation. To do this, in the above script just ctrl_dof = np.array([True, True, True, True, True, True]), and there you go! In the following animations the gain values used were kp=300, ko=300, and kv=np.sqrt(kp+ko)*1.5. The full script can be found up on my GitHub.

• 

  Method 1 – Stack overflow code

• 

  Method 2 – Caccavale quaternion

• 

  Method 3 – Caccavale angle/axis

• 

  Method 4 – Yuan / Nakanishi

NOTE: Setting the gains properly for this task is pretty critical, and I did it just by trial and error until I got something that was decent for each. For a real comparison, better parameter tuning would have to be undertaken more rigorously. 

NOTE: When implementing this minimal code example script I ran into a problem that was caused by the task-space inertia matrix calculation. It turns out that using np.linalg.pinv gives very different results than np.linalg.inv, and I did not realise this. I’m going to have to explore this more fully later, but basically heads up that you want to be using np.linalg.inv as much as possible. So you’ll notice in the above code I check the dimensionality of Mx_inv and first try to use np.linalg.inv before resorting to np.linalg.pinv.

NOTE: If you start playing around with controlling only one or two of the orientation angles, something to keep in mind: Because we’re using rotating axes, if you set up False, False, True then it’s not going to look like of the end-effector is lining up with the of the target. This is because and weren’t set first. If you generate a plot of the target orientations vs the end-effector orientations, however, you’ll see that you are in face reaching the target orientation for .

In summary

So that’s that! Lots of caveats, notes, and more work to be done, but hopefully this will be a useful resource for any others embarking on the same journey. You can download the code, try it out, and play around with the gains and targets. Let me know below if you have any questions or enjoyed the post, or want to share any other resources on force control of task-space orientation.

And once again thanks to Yitao Ding for his helpful comments and corrections on the original version of this article.

Full body obstacle collision avoidance

Previously I’ve discussed how to avoid obstacles using DMPs in the end-effector trajectory. This is good when you’re controlling a single disconnected point-mass, like a mobile robot navigating around an environment. But if you want to use this system to control a robotic manipulator, then pretty quickly you run into the problem that your end-effector is not a disconnected point-mass moving around the environment. It’s attached to the rest of the arm, and moving such that the arm segments and joints also avoid the obstacle is a whole other deal.

I was doing a quick lit scan on methods for control methods for avoiding joint collision with obstacles, and was kind of surprised that there wasn’t really much in the realm of recent discussions about it. There is, however, a 1986 paper from Dr. Oussama Khatib titled Real-time obstacle avoidance for manipulators and mobile robots that pretty much solves this problem short of getting into explicit path planning methods. Which could be why there aren’t papers since then about it. All the same, I couldn’t find any implementations of it online, and there are a few tricky parts, so in this post I’m going to work through the implementation.

Note: The implementation that I’ve worked out here uses spheres to represent the obstacles. This works pretty well in general by just making the sphere large enough to cover whatever obstacle you’re avoiding. But if you want a more precise control around other shapes, you can check out the appendix of Dr. Khatib’s paper, where he works provides the math for cubes and cones as well.

Note: You can find all of the code I use here and everything you need for the VREP implementation up on my GitHub. I’ve precalculated the functions that are required, because generating them is quite computationally intensive. Hopefully the file saving doesn’t get weird between different operating systems, but if it does, try deleting all of the files in the ur5_config folder and running the code again. This will regenerate those files (on my laptop this takes ~4 hours, though, so beware).

The general idea

Since it’s from Dr. Khatib, you might expect that this approach involves task space. And indeed, your possible suspicions are correct! The algorithm is going to work by identifying forces in Cartesian coordinates that will move any point of the arm that’s too close to an obstacle away from it. The algorithm follows the form:

Setup

• Specify obstacle location and size
• Specify a threshold distance to the obstacle

While running

• Find the closest point of each arm segment to obstacles
• If within threshold of obstacle, generate force to apply to that point
• Transform this force into joint torques
• Add directly to the outgoing control signal

Something that you might notice about this is that it’s similar to the addition of the null space controller that we’ve seen before in operational space control. There’s a distinct difference here though, in that the control signal for avoiding obstacles is added directly to the outgoing control signal, and that it’s not filtered (like the null space control signal) such that there’s no guarantee that it won’t affect the movement of the end-effector. In fact, it’s very likely to affect the movement of the end-effector, but that’s also desirable, as not ramming the arm through an obstacle is as important as getting to the target.

OK, let’s walk through these steps one at a time.

Setup

I mentioned that we’re going to treat all of our obstacles as spheres. It’s actually not much harder to do these calculations for cubes too, but this is already going to be long enough so I’m only addressing sphere’s here. This algorithm assumes we have a list of every obstacle’s centre-point and radius.

We want the avoidance response of the system to be a function of the distance to the obstacle, such that the closer the arm is to the obstacle the stronger the response. The function that Dr. Khatib provides is of the following form:

where is the distance to the target, is the threshold distance to the target at which point the avoidance function activates, is the partial derivative of the distance to the target with respect to a given point on the arm, and is a gain term.

This function looks complicated, but it’s actually pretty intuitive. The partial derivative term in the function works simply to point in the opposite direction of the obstacle, in Cartesian coordinates, i.e. tells the system how to get away from the obstacle. The rest of the term is just a gain that starts out at zero when , and gets huge as the obstacle nears the object (as ). Using and gives us a function that looks like

So you can see that very quickly a very, very strong push away from this obstacle is going to be generated once we enter the threshold distance. But how do we know exactly when we’ve entered the threshold distance?

Find the closest point

We want to avoid the obstacle with our whole body, but it turns out we can reduce the problem to only worrying about the closest point of each arm segment to the obstacle, and move that one point away from the obstacle if threshold distance is hit.

To find the closest point on a given arm segment to the obstacle we’ll do some pretty neat trig. I’ll post the code for it and then discuss it below. In this snippet, p1 and p2 are the beginning and ending locations of arm segment (which we are assuming is a straight line), and v is the center of the obstacle.

# the vector of our line
vec_line = p2 - p1
# the vector from the obstacle to the first line point
vec_ob_line = v - p1
# calculate the projection normalized by length of arm segment
projection = (np.dot(vec_ob_line, vec_line) /
              np.dot(vec_line, vec_line))
if projection < 0:               
    # then closest point is the start of the segment
    closest = p1  
elif projection > 1:
    # then closest point is the end of the segment
    closest = p2
else:
    closest = p1 + projection * vec_line

The first thing we do is find the arm segment line, and then line from the obstacle center to the start point of the arm segment. Once we have these, we do:

using the geometric definition of the dot product two vectors, we can rewrite the above as

which reads as the magnitude of vec_ob_line divided by the magnitude of vec_line (I know, these are terrible names, sorry) multiplied by the angle between the two vectors. If the angle between the vectors is < 0 (projection will also be < 0), then right off the bat we know that the start of the arm segment, p1, is the closest point. If the projection value is > 1, then we know that 1) the length from the start of the arm segment to the obstacle is longer than the length of the arm, and 2) the angle is such that the end of the arm segment, p2, is the closest point to the obstacle.

Finally, in the last case we know that the closest point is somewhere along the arm segment. To find where exactly, we do the following

which can be rewritten

I find it more intuitive if we rearrange the second term to be

So then what this is all doing is starting us off at the beginning of the arm segment, p1, and to that we add this other fun term. The first part of this fun term provides direction normalized to magnitude 1. The second part of this term provides magnitude, specifically the exact distance along vec_line we need to traverse to form reach a right angle (giving us the shortest distance) pointing at the obstacle. This handy figure from the Wikipedia page helps illustrate exactly what’s going on with the second part, where B is be vec_line and A is vec_ob_line:

Armed with this information, we understand how to find the closest point of each arm segment to the obstacle, and we are now ready to generate a force to move the arm in the opposite direction!

Check distance, generate force

To calculate the distance, all we have to do is calculate the Euclidean distance from the closest point of the arm segment to the center of the sphere, and then subtract out the radius of the sphere:

# calculate distance from obstacle vertex to the closest point
dist = np.sqrt(np.sum((v - closest)**2))
# account for size of obstacle
rho = dist - obstacle[3]

Once we have this, we can check it and generate using the equation we defined above. The one part of that equation that wasn’t specified was exactly what was. Since it’s just the partial derivative of the distance to the target with respect to the closest point, we can calculate it as the normalized difference between the two points:

drhodx = (v - closest) / rho

Alright! Now we’ve found the closest point, and know the force we want to apply, from here it’s standard operational space procedure.

Transform the force into torques

As we all remember, the equation for transforming a control signal from operational space to involves two terms aside from the desired force. Namely, the Jacobian and the operational space inertia matrix:

where is the Jacobian for the point of interest, is the operational space inertia matrix for the point of interest, and is the force we defined above.

Calculating the Jacobian for an unspecified point

So the first thing we need to calculate is the Jacobian for this point on the arm. There are a bunch of ways you could go about this, but the way I’m going to do it here is by building on the post where I used SymPy to automate the Jacobian derivation. The way we did that was by defining the transforms from the origin reference frame to the first link, from the first link to the second, etc, until we reached the end-effector. Then, whenever we needed a Jacobian we could string together the transforms to get the transform from the origin to that point on the arm, and take the partial derivative with respect to the joints (using SymPy’s derivative method).

As an example, say we wanted to calculate the Jacobian for the third joint, we would first calculate:

where reads the transform from reference frame to reference frame .

Once we have this transformation matrix, , we multiply it by the point of interest in reference frame 3, which, previously, has usually been . In other words, usually we’re just interested in the origin of reference frame 3. So the Jacobian is just

what if we’re interested in some non-specified point along link 3, though? Well, using SymPy we set make instead of (recall the 1 at the end in these vectors is just to make the math work), and make the Jacobian function SymPy generates for us dependent on both and , rather than just . In code this looks like:

Torg3 = self._calc_T(name="3")
# transform x into world coordinates
Torg3x = sp.simplify(Torg3 * sp.Matrix(x))
J3_func = sp.lambdify(q + x, Torg3)

Now it’s possible to calculate the Jacobian for any point along link 3 just by changing the parameters that we pass into J3_func! Most excellent.

We are getting closer.

NOTE: This parameterization can significantly increase the build time of the function, it took my laptop about 4 hours. To decrease build time you can try commenting out the simplify calls from the code, which might slow down run-time a bit but significantly drops the generation time.

Where is the closest point in that link’s reference frame?

A sneaky problem comes up when calculating the closest point of each arm segment to the object: We’ve calculated the closest point of each arm segment in the origin’s frame of reference, and we need thew relative to each link’s own frame of reference. Fortunately, all we have to do is calculate the inverse transform for the link of interest. For example, the inverse transform of transforms a point from the origin’s frame of reference to the reference frame of the 3rd joint.

I go over how to calculate the inverse transform at the end of my post on forward transformation matrices, but to save you from having to go back and look through that, here’s the code to do it:

Torg3 = self._calc_T(name="3")
rotation_inv = Torg3[:3, :3].T
translation_inv = -rotation_inv * Torg3[:3, 3]
Torg3_inv = rotation_inv.row_join(translation_inv).col_join(
    sp.Matrix([[0, 0, 0, 1]]))

And now to find the closest point in the coordinates of reference frame 3 we simply

x = np.dot(Torg3_inv, closest)

This x value is what we’re going to plug in as parameters to our J3_func above to find the Jacobian for the closest point on link 3.

Calculate the operational space inertia matrix for the closest point

OK. With the Jacobian for the point of interest we are now able to calculate the operational space inertia matrix. This code I’ve explicitly worked through before, and I’ll show it in the full code below, so I won’t go over it again here.

The whole implementation

You can run an example of all this code controlling the UR5 arm to avoid obstacles in VREP using this code up on my GitHub. The specific code added to implement obstacle avoidance looks like this:

# find the closest point of each link to the obstacle
for ii in range(robot_config.num_joints):
    # get the start and end-points of the arm segment
    p1 = robot_config.Tx('joint%i' % ii, q=q)
    if ii == robot_config.num_joints - 1:
        p2 = robot_config.Tx('EE', q=q)
    else:
        p2 = robot_config.Tx('joint%i' % (ii + 1), q=q)

    # calculate minimum distance from arm segment to obstacle
    # the vector of our line
    vec_line = p2 - p1
    # the vector from the obstacle to the first line point
    vec_ob_line = v - p1
    # calculate the projection normalized by length of arm segment
    projection = (np.dot(vec_ob_line, vec_line) /
                  np.sum((vec_line)**2))
    if projection < 0:         
        # then closest point is the start of the segment
        closest = p1
    elif projection > 1:
        # then closest point is the end of the segment
        closest = p2
    else:
        closest = p1 + projection * vec_line
    # calculate distance from obstacle vertex to the closest point
    dist = np.sqrt(np.sum((v - closest)**2))
    # account for size of obstacle
    rho = dist - obstacle_radius

    if rho < threshold:
        eta = .02
        drhodx = (v - closest) / rho
        Fpsp = (eta * (1.0/rho - 1.0/threshold) *
                1.0/rho**2 * drhodx)

        # get offset of closest point from link's reference frame
        T_inv = robot_config.T_inv('link%i' % ii, q=q)
        m = np.dot(T_inv, np.hstack([closest, [1]]))[:-1]
        # calculate the Jacobian for this point
        Jpsp = robot_config.J('link%i' % ii, x=m, q=q)[:3]

        # calculate the inertia matrix for the
        # point subjected to the potential space
        Mxpsp_inv = np.dot(Jpsp,
                        np.dot(np.linalg.pinv(Mq), Jpsp.T))
        svd_u, svd_s, svd_v = np.linalg.svd(Mxpsp_inv)
        # cut off singular values that could cause problems
        singularity_thresh = .00025
        for ii in range(len(svd_s)):
            svd_s[ii] = 0 if svd_s[ii] < singularity_thresh else \
                1./float(svd_s[ii])
        # numpy returns U,S,V.T, so have to transpose both here
        Mxpsp = np.dot(svd_v.T, np.dot(np.diag(svd_s), svd_u.T))

        u_psp = -np.dot(Jpsp.T, np.dot(Mxpsp, Fpsp))
        if rho < .01:
            u = u_psp
        else:
            u += u_psp

The one thing in this code I didn’t talk about is that you can see that if rho < .01 then I set u = u_psp instead of just adding u_psp to u. What this does is basically add in a fail safe take over of the robotic control saying that “if we are about to hit the obstacle forget about everything else and get out of the way!”.

Results

And that’s it! I really enjoy how this looks when it’s running, it’s a really effective algorithm. Let’s look at some samples of it in action.

First, in a 2D environment, where it’s real easy to move around the obstacle and see how it changes in response to the new obstacle position. The red circle is the target and the blue circle is the obstacle:

And in 3D in VREP, running the code example that I’ve put up on my GitHub implementing this. The example of it running without obstacle avoidance code is on the left, and running with obstacle avoidance is on the right. It’s kind of hard to see but on the left the robot moves through the far side of the obstacle (the gold sphere) on its way to the target (the red sphere):

And one last example, the arm dodging a moving obstacle on its way to the target.

The implementation is a ton of fun to play around with. It’s a really nifty algorithm, that works quite well, and I haven’t found many alternatives in papers that don’t go into path planning (if you know of some and can share that’d be great!). This post was a bit of a journey, but hopefully you found it useful! I continue to find it impressive how many different neat features like this can come about once you have the operational space control framework in place.

Velocity limiting in operational space control

Recently, I was reading through an older paper on effective operational space control, talking specifically point to point control in operational space. The paper mentioned that even if you have a perfect model of the system, you’re going to run into trouble if you use just a basic PD formula to define your control signal in operational space:

where and are the system position and velocity in operational space, is the target position, and and are gains.

If you define your operational space control signal like this, and then translate this signal into joint torques (using, for example, methods discussed in other posts), you’re going to see a very non-straight trajectory emerge in larger movements as a result of “actuator saturation, and bandwidth and velocity limitations”. In the example of a standard robot, you might run into issues with your motors not being able to actually generate the torques that have been specified, the frequency of control and feedback might not be sufficient, and you could hit hard constraints on system velocity. The solution to this problem was presented in this 1987 paper by Dr. Oussama Khatib, and is pretty slick and very useful, so I thought I’d write it up here for any other unfortunate souls wandering around in ignorance. First though, here’s what it looks like to move large point to point distances without velocity limiting:

As you can see, the system isn’t moving in a straight line, which can be very aggravating if you’ve worked and reworked out the equations and double checked all your parameters, etc etc. A few things, first, when working with simulations it’s easy to forget how ridiculously fast this actually would be in real-time. Even though it takes a minute to simulate the above movement, in real-time, is happening over the course of 200ms. Taking that into account, this is pretty good. Also, there’s an obvious solution here, slow down your movement. The source of this problem is largely that all of the motors are not able to apply the torques specified and move at the required speed. Some of the motors have a lot less mass to throw around and will be able to move at the specified torques, but not all. Hence the not straight trajectory.

You can of course drop the gains on your PD signal, but that’s not really a great methodical solution. So, what can we do?

Well, if we rearrange the PD control signal specified above into

where is the desired velocity, we see that this signal can be interpreted as a pure velocity servo-control signal, with velocity gain and a desired velocity

.

When things are in this form, it becomes a bit more clear what we have to do: limit the desired velocity to be at most some specified maximum velocity of the end-effector, . This value should be low enough that the transformation into joint torques doesn’t result in anything larger than the actuators can generate.

Taking , what we want is to clip the magnitude of the control signal to be if it’s ever larger (in positive or negative directions), and to be equal to otherwise. The math for this works out such that we can accomplish this with a control signal of the form:

,

where , , and is the saturation function, such that

where is the absolute value of , and is applied element wise to the vector in the control signal.

As a result of using this saturation function, the control signal behaves differently depending on whether or not :

where is a function that returns -1 if and 1 if , and is again applied element-wise to vectors. Note that the control signal in the second condition is equivalent to our original PD control signal . If you’re wondering about negative signs make sure you note that and not , as you might assume.

So now the control signal is behaving exactly as desired! Moves the system towards the target, but no faster than the specified maximum velocity. Now our trajectories look like this:

So those are starting to look a lot better! The first thing you’ll notice is that this is a fair bit slower of a movement. Well, actually, it’s waaaayyyy slower because the playback speed here is 4x faster than in that first animation, and this is a movement over 2s. Which has pros and cons, con: it’s slower, pro: it’s straighter, and you’re less likely to be murdered by it. When you move from simulations to real systems that latter point really moves way up the priority list.

Second thing to notice, the system seems to be minimising the error along one dimension, and then along the next, and then arrives at the target. What’s going on?  Because the error along each of the dimensions isn’t the same, when speed gets clipped along one of the dimensions you’re no longer going to be moving in a straight line directly to the target. To address this, we’re going to add a scaling term whenever clipping happens, such that you reduce the speed you move along each dimension by the same ratio, so that you’re still moving in a straight line.

It’s a liiiiittle bit more complicated than that, but not much. First, we’ll calculate the values being passed in to the saturation function for each dimension. We’ll then check to see if any of them are going to get clipped, and if there’s more than one that saturates we’ll find the one that is affected the most. After we’ve identified which dimension it is, we go through and calculate what the control signal would have been without velocity limiting, and what it will be now with velocity limiting. This scaling term tells us how much the control signal was reduced, and we can then use it to reduce the control signals of the other dimensions by the same amount. These other dimensions might still saturate, though, so we have to recalculate the saturation function for them once they’ve been scaled. Here’s what this all looks like in code:

# implement velocity limiting
lamb = kp / kv
x_tilde = xyz - target_xyz
sat = vmax / (lamb * np.abs(x_tilde))
scale = np.ones(3)
if np.any(sat < 1):
    index = np.argmin(sat)
    unclipped = kp * x_tilde[index]
    clipped = kv * vmax * np.sign(x_tilde[index])
    scale = np.ones(3) * clipped / unclipped
    scale[index] = 1
u_xyz = -kv * (dx + np.clip(sat / scale, 0, 1) *
               scale * lamb * x_tilde)
 

And now, finally, we start getting the trajectories that we’ve been wanting the whole time:

And finally we can rest easy, knowing that our robot is moving at a reasonable speed along a direct path to its goals. Wherever you’d like to use this neato ‘ish you should be able to just paste in the above code, define your vmax, kp, and kv values and be good to go!

Dynamic movement primitives part 4: Avoiding obstacles – update

Edit: Previously I posted this blog post on incorporating obstacle avoidance, but after a recent comment on the code I started going through it again and found a whole bunch of issues. Enough so that I’ve recoded things and I’m going to repost it now with working examples and a description of the changes I made to get it going. The edited sections will be separated out with these nice horizontal lines. If you’re just looking for the example code, you can find it up on my pydmps repo, here.

---

Alright. Previously I’d mentioned in one of these posts that DMPs are awesome for generalization and extension, and one of the ways that they can be extended is by incorporating obstacle avoidance dynamics. Recently I wanted to implement these dynamics, and after a bit of finagling I got it working, and so that’s going to be the subject of this post.

There are a few papers that talk about this, but the one we’re going to use is Biologically-inspired dynamical systems for movement generation: automatic real-time goal adaptation and obstacle avoidance by Hoffmann and others from Stefan Schaal’s lab. This is actually the second paper talking about obstacle avoidance and DMPs, and this is a good chance to stress one of the most important rules of implementing algorithms discussed in papers: collect at least 2-3 papers detailing the algorithm (if possible) before attempting to implement it. There are several reasons for this, the first and most important is that there are likely some typos in the equations of one paper, by comparing across a few papers it’s easier to identify trickier parts, after which thinking through what the correct form should be is usually straightforward. Secondly, often equations are updated with simplified notation or dynamics in later papers, and you can save yourself a lot of headaches in trying to understand them just by reading a later iteration. I recklessly disregarded this advice and started implementation using a single, earlier paper which had a few key typos in the equations and spent a lot of time tracking down the problem. This is just a peril inherent in any paper that doesn’t provide tested code, which is almost all, sadface.

OK, now on to the dynamics. Fortunately, I can just reference the previous posts on DMPs here and don’t have to spend any time discussing how we arrive at the DMP dynamics (for a 2D system):

where and are gain terms, is the goal state, is the system state, is the system velocity, and is the forcing function.
As mentioned, DMPs are awesome because now to add obstacle avoidance all we have to do is add another term

where implements the obstacle avoidance dynamics, and is a function of the DMP state and velocity. Now then, the question is what are these dynamics exactly?

Obstacle avoidance dynamics

It turns out that there is a paper by Fajen and Warren that details an algorithm that mimics human obstacle avoidance. The idea is that you calculate the angle between your current velocity and the direction to the obstacle, and then turn away from the obstacle. The angle between current velocity and direction to the obstacle is referred to as the steering angle, denoted , here’s a picture of it:

So, given some value, we want to specify how much to change our steering direction, , as in the figure below:

If we’re on track to hit the object (i.e. is near 0) then we steer away hard, and then make your change in direction less and less as the angle between your heading (velocity) and the object is larger and larger. Formally, define as

where and are constants, which are specified as and in the paper, respectively.

---

Edit: OK this all sounds great, but quickly you run into issues here. The first is how do we calculate ? In the paper I was going off of they used a dot product between the vector and the vector to get the cosine of the angle, and then use np.arccos to get the angle from that. There is a big problem with this here, however, that’s kind of subtle: You will never get a negative angle when you calculate this, which, of course. That’s not how np.arccos works, but it is still what we need so we will be able to tell if we should be turning left or right to avoid this object!

So we need to use a different way of calculating the angle, one that tells us if the object is in a + or – angle relative to the way we’re headed. To calculate an angle that will give us + or -, we’re going to use the np.arctan2 function.

We want to center things around the way we’re headed, so first we calculate the angle of the direction vector, . Then we create a rotation vector, R_dy to rotate the vector describing the direction of the object. This shifts things around so that if we’re moving straight towards the object it’s at 0 degrees, if we’re headed directly away from it, it’s at 180 degrees, etc. Once we have that vector, nooowwww we can find the angle of the direction of the object and that’s what we’re going to use for phi. Huzzah!

# get the angle we're heading in
phi_dy = -np.arctan2(dy[1], dy[0]) 
R_dy = np.array([[np.cos(phi_dy), -np.sin(phi_dy)],
                 [np.sin(phi_dy), np.cos(phi_dy)]])
# calculate vector to object relative to body
obj_vec = obstacle - y
# rotate it by the direction we're going 
obj_vec = np.dot(R_dy, obj_vec)
# calculate the angle of obj relative to the direction we're going
phi = np.arctan2(obj_vec[1], obj_vec[0])

---

This term can be thought of as a weighting, telling us how much we need to rotate based on how close we are to running into the object. To calculate how we should rotate we’re going to calculate the angle orthonormal to our current velocity, then weight it by the distance between the object and our current state on each axis. Formally, this is written:

where is the axis rotated 90 degrees (the denoting outer product here). The way I’ve been thinking about this is basically taking your velocity vector, , and rotating it 90 degrees. Then we use this rotated vector as a row vector, and weight the top row by the distance between the object and the system along the axis, and the bottom row by the difference along the axis. So in the end we’re calculating the angle that rotates our velocity vector 90 degrees, weighted by distance to the object along each axis.

So that whole thing takes into account absolute distance to object along each axis, but that’s not quite enough. We also need to throw in , which looks at the current angle. What this does is basically look at ‘hey are we going to hit this object?’, if you are on course then make a big turn and if you’re not then turn less or not at all. Phew.

OK so all in all this whole term is written out

and that’s what we add in to the system acceleration. And now our DMP can avoid obstacles! How cool is that?

Super compact, straight-forward to add, here’s the code:

---

Edit: OK, so not suuuper compact. I’ve also added in another couple checks. The big one is “Is this obstacle between us and the target or not?”. So I calculate the Euclidean distance to the goal and the obstacle, and if the obstacle is further away then the goal, set the avoidance signal to zero (performed at the end of the if)! This took care of a few weird errors where you would get a big deviation in the trajectory if it saw an obstacle past the goal, because it was planning on avoiding it, but then was pulled back in to the goal before the obstacle anyways so it was a pointless exercise. The other check added in is just to make sure you only add in obstacle avoidance if the system is actually moving. Finally, I also changed the instead of .

---

def avoid_obstacles(y, dy, goal):
    p = np.zeros(2)
 
    for obstacle in obstacles:
        # based on (Hoffmann, 2009)

        # if we're moving
        if np.linalg.norm(dy) > 1e-5:

            # get the angle we're heading in
            phi_dy = -np.arctan2(dy[1], dy[0]) 
            R_dy = np.array([[np.cos(phi_dy), -np.sin(phi_dy)],
                             [np.sin(phi_dy), np.cos(phi_dy)]])
            # calculate vector to object relative to body
            obj_vec = obstacle - y
            # rotate it by the direction we're going 
            obj_vec = np.dot(R_dy, obj_vec)
            # calculate the angle of obj relative to the direction we're going
            phi = np.arctan2(obj_vec[1], obj_vec[0])

            dphi = gamma * phi * np.exp(-beta * abs(phi))
            R = np.dot(R_halfpi, np.outer(obstacle - y, dy))
            pval = -np.nan_to_num(np.dot(R, dy) * dphi)

            # check to see if the distance to the obstacle is further than 
            # the distance to the target, if it is, ignore the obstacle
            if np.linalg.norm(obj_vec) > np.linalg.norm(goal - y):
                pval = 0

            p += pval
    return p

And that’s it! Just add this method in to your DMP system and call avoid_obstacles at every timestep, and add it in to your DMP acceleration.

You hopefully noticed in the code that this is set up for multiple obstacles, and that all that that entailed was simply adding the p value generated by each individual obstacle. It’s super easy! Here’s a very basic graphic showing how the DMP system can avoid obstacles:

So here there’s just a basic attractor system (DMP without a forcing function) trying to move from the center position to 8 targets around the unit circle (which are highlighted in red), and there are 4 obstacles that I’ve thrown onto the field (black x’s). As you can see, the system successfully steers way clear of the obstacles while moving towards the target!

We must all use this power wisely.

---

Edit: Making the power yours is now easier than ever! You can check out this code at my pydmps GitHub repo. Clone the repo and after you python setup.py develop, change directories into the examples folder and run the avoid_obstacles.py file. It will randomly generate 5 targets in the environment and perform 20 movements, giving you something looking like this:

---

Operational space control of 6DOF robot arm with spiking cameras part 2: Deriving the Jacobian

In the previous exciting post in this series I outlined the project, which is in the title, and we worked through getting access to the arm through Python. The next step was deriving the Jacobian, and that’s what we’re going to be talking about in this post!

Alright.
This was a time I was very glad to have a previous post talking about generating transformation matrices, because deriving the Jacobian for a 6DOF arm in 3D space comes off as a little daunting when you’re used to 3DOF in 2D space, and I needed a reminder of the derivation process. The first step here was finding out which motors were what, so I went through and found out how each motor moved with something like the following code:

for ii in range(7):
    target_angles = np.zeros(7, dtype='float32')
    target_angles[ii] = np.pi / 4.0
    rob.move(target_angles)
    time.sleep(1)

and I found that the robot is setup in the figures below

this is me trying my hand at making things clearer using Inkscape, hopefully it’s worked. Displayed are the first 6 joints and their angles of rotation, through . The 7th joint, , opens and closes the gripper, so we’re safe to ignore it in deriving our Jacobian. The arm segment lengths and are named based on the nearest joint angles (makes easier reading in the Jacobian derivation).

Find the transformation matrix from end-effector to origin

So first thing’s first, let’s find the transformation matrices. Our first joint, , rotates around the axis, so the rotational part of our transformation matrix is

and and our origin frame of reference are on top of each other so we don’t need to account for translation, so our translation component of is

Stacking these together to form our first transformation matrix we have

So now we are able to convert a position in 3D space from to the reference frame of joint back to our origin frame of reference. Let’s keep going.

Joint rotates around the axis, and there is a translation along the arm segment . Our transformation matrix looks like

Joint also rotates around the axis, but there is no translation from to . So our transformation matrix looks like

The next transformation matrix is a little tricky, because you might be tempted to say that it’s rotating around the axis, but actually it’s rotating around the axis. This is determined by where is mounted relative to . If it was mounted at 90 degrees from then it would be rotating around the axis, but it’s not. For translation, there’s a translation along the axis up to the next joint, so all in all the transformation matrix looks like:

And then the transformation matrices for coming from to and to are the same as the previous set, so we have

and

Alright! Now that we have all of the transformation matrices, we can put them together to get the transformation from end-effector coordinates to our reference frame coordinates!

At this point I went and tested this with some sample points to make sure that everything seemed to be being transformed properly, but we won’t go through that here.

Calculate the derivative of the transform with respect to each joint

The next step in calculating the Jacobian is getting the derivative of . This could be a big ol’ headache to do it by hand, OR we could use SymPy, the symbolic computation package for Python. Which is exactly what we’ll do. So after a quick

sudo pip install sympy

I wrote up the following script to perform the derivation for us

import sympy as sp

def calc_transform():
    # set up our joint angle symbols (6th angle doesn't affect any kinematics)
    q = [sp.Symbol('q0'), sp.Symbol('q1'), sp.Symbol('q2'), sp.Symbol('q3'),
            sp.Symbol('q4'), sp.Symbol('q5')]
    # set up our arm segment length symbols
    l1 = sp.Symbol('l1')
    l3 = sp.Symbol('l3')
    l5 = sp.Symbol('l5')

    Torg0 = sp.Matrix([[sp.cos(q[0]), -sp.sin(q[0]), 0, 0,],
                       [sp.sin(q[0]), sp.cos(q[0]), 0, 0],
                       [0, 0, 1, 0],
                       [0, 0, 0, 1]])

    T01 = sp.Matrix([[1, 0, 0, 0],
                     [0, sp.cos(q[1]), -sp.sin(q[1]), l1*sp.cos(q[1])],
                     [0, sp.sin(q[1]), sp.cos(q[1]), l1*sp.sin(q[1])],
                     [0, 0, 0, 1]])

    T12 = sp.Matrix([[1, 0, 0, 0],
                     [0, sp.cos(q[2]), -sp.sin(q[2]), 0],
                     [0, sp.sin(q[2]), sp.cos(q[2]), 0],
                     [0, 0, 0, 1]])

    T23 = sp.Matrix([[sp.cos(q[3]), 0, sp.sin(q[3]), 0],
                     [0, 1, 0, l3],
                     [-sp.sin(q[3]), 0, sp.cos(q[3]), 0],
                     [0, 0, 0, 1]])

    T34 = sp.Matrix([[1, 0, 0, 0],
                     [0, sp.cos(q[4]), -sp.sin(q[4]), 0],
                     [0, sp.sin(q[4]), sp.cos(q[4]), 0],
                     [0, 0, 0, 1]])

    T45 = sp.Matrix([[sp.cos(q[5]), 0, sp.sin(q[5]), 0],
                     [0, 1, 0, l5],
                     [-sp.sin(q[5]), 0, sp.cos(q[5]), 0],
                     [0, 0, 0, 1]])

    T = Torg0 * T01 * T12 * T23 * T34 * T45

    # position of the end-effector relative to joint axes 6 (right at the origin)
    x = sp.Matrix([0,0,0,1])

    Tx = T * x

    for ii in range(6):
        print q[ii]
        print sp.simplify(Tx[0].diff(q[ii]))
        print sp.simplify(Tx[1].diff(q[ii]))
        print sp.simplify(Tx[2].diff(q[ii]))

And then consolidated the output using some variable shorthand to write a function that accepts in joint angles and generates the Jacobian:

def calc_jacobian(q):
    J = np.zeros((3, 7))

    c0 = np.cos(q[0])
    s0 = np.sin(q[0])
    c1 = np.cos(q[1])
    s1 = np.sin(q[1])
    c3 = np.cos(q[3])
    s3 = np.sin(q[3])
    c4 = np.cos(q[4])
    s4 = np.sin(q[4])

    c12 = np.cos(q[1] + q[2])
    s12 = np.sin(q[1] + q[2])

    l1 = self.l1
    l3 = self.l3
    l5 = self.l5

    J[0,0] = -l1*c0*c1 - l3*c0*c12 - l5*((s0*s3 - s12*c0*c3)*s4 + c0*c4*c12)
    J[1,0] = -l1*s0*c1 - l3*s0*c12 + l5*((s0*s12*c3 + s3*c0)*s4 - s0*c4*c12)
    J[2,0] = 0

    J[0,1] = (l1*s1 + l3*s12 + l5*(s4*c3*c12 + s12*c4))*s0
    J[1,1] = -(l1*s1 + l3*s12 + l5*s4*c3*c12 + l5*s12*c4)*c0
    J[2,1] = l1*c1 + l3*c12 - l5*(s4*s12*c3 - c4*c12)

    J[0,2] = (l3*s12 + l5*(s4*c3*c12 + s12*c4))*s0
    J[1,2] = -(l3*s12 + l5*s4*c3*c12 + l5*s12*c4)*c0
    J[2,2] = l3*c12 - l5*(s4*s12*c3 - c4*c12)

    J[0,3] = -l5*(s0*s3*s12 - c0*c3)*s4
    J[1,3] = l5*(s0*c3 + s3*s12*c0)*s4
    J[2,3] = -l5*s3*s4*c12

    J[0,4] = l5*((s0*s12*c3 + s3*c0)*c4 + s0*s4*c12)
    J[1,4] = l5*((s0*s3 - s12*c0*c3)*c4 - s4*c0*c12)
    J[2,4] = -l5*(s4*s12 - c3*c4*c12)

    return J

Alright! Now we have our Jacobian! Really the only time consuming part here was calculating our end-effector to origin transformation matrix, generating the Jacobian was super easy using SymPy once we had that.

Hack position control using the Jacobian

Great! So now that we have our Jacobian we’ll be able to translate forces that we want to apply to the end-effector into joint torques that we want to apply to the arm motors. Since we can’t control applied force to the motors though, and have to pass in desired angle positions, we’re going to do a hack approximation. Let’s first transform our forces from end-effector space into a set of joint angle torques:

To approximate the control then we’re simply going to take the current set of joint angles (which we know because it’s whatever angles we last told the system to move to) and add a scaled down version of to approximate applying torque that affects acceleration and then velocity.

where is the gain term, I used .001 here because it was nice and slow, so no crazy commands that could break the servos would be sent out before I could react and hit the cancel button.

What we want to do then to implement operational space control here then is find the current position of the end-effector, calculate the difference between it and the target end-effector position, use that to generate the end-effector control signal , get the Jacobian for the current state of the arm using the function above, find the set of joint torques to apply, approximate this control by generating a set of target joint angles to move to, and then repeat this whole loop until we’re within some threshold of the target position. Whew.

So, a lot of steps, but pretty straight forward to implement. The method I wrote to do it looks something like:

def move_to_xyz(self, xyz_d):
    """
    np.array xyz_d: 3D target (x_d, y_d, z_d)
    """
    count = 0
    while (1):
        count += 1
        # get control signal in 3D space
        xyz = self.calc_xyz()
        delta_xyz = xyz_d - xyz
        ux = self.kp * delta_xyz

        # transform to joint space
        J = self.calc_jacobian()
        u = np.dot(J.T, ux)

        # target joint angles are current + uq (scaled)
        self.q[...] += u * .001
        self.robot.move(np.asarray(self.q.copy(), 'float32'))

        if np.sqrt(np.sum(delta_xyz**2)) < .1 or count > 1e4:
            break

And that is it! We have successfully hacked together a system that can perform operational space control of a 6DOF robot arm. Here is a very choppy video of it moving around to some target points in a grid on a cube.

So, granted I had to drop a lot of frames from the video to bring it’s size down to something close to reasonable, but still you can see that it moves to target locations super fast!

Alright this is sweet, but we’re not done yet. We don’t want to have to tell the arm where to move ourselves. Instead we’d like the robot to perform target tracking for some target LED we’re moving around, because that’s way more fun and interactive. To do this, we’re going to use spiking cameras! So stay tuned, we’ll talk about what the hell spiking cameras are and how to use them for a super quick-to-setup and foolproof target tracking system in the next exciting post!

Dynamic movement primitives part 2: Controlling end-effector trajectories

The dynamic movement primitive (DMP) framework was designed for trajectory control. It so happens that in previous posts we’ve built up to having several arm simulations that are ripe for throwing a trajectory controller on top, and that’s what we’ll do in this post. The system that we will be controlling here is the 3 link arm model with an operational space controller (OSC) that translates end-effector forces into joint torques. The DMPs here will be controlling the trajectory of the hand, and the OSC will take care of turning the desired hand forces into torques that can be applied to the arm. All of the code used to generate the animations throughout this post can of course be found up on my github (to run play around with variants of python run.py arm3 dmp write).

Controlling a 3 link arm with DMPs
We have our 3 link arm and its OSC controller; this whole setup we’ll collectively refer to as ‘the plant’ throughout this post. We are going to pass in some force signal to the plant, and the plant will carry it out. Additionally we’ll get a feedback signal with the position of the hand. At the same time, we also have a DMP system that’s doing its own thing, tracing out a desired trajectory in space. We have to tie these two systems together.

To do this is easy, we’ll generate the control signal for the plant from our DMP system simply by measuring the difference between the state of our DMP system and the plant state, use that to drive the plant to the state of the DMP system. Formally,

where is the state of the DMP system, is the state of the plant, and and is the position error gain term.

Once we have this, we just go ahead and step our DMP system forward and make sure the gain values on the control signal are high enough that the plant follows the DMP’s trajectory. And that’s pretty much it, just run the DMP system to the end of the trajectory and then stop your simulation.

To give a demonstration of DMP control I’ve set up the DMP system to follow the same number trajectories that the SPAUN arm followed. As you can see the combination of DMPs and operational space control is much more effective than my previous implementation.

Incorporating system feedback

One of the issues in implementing the control above is that we have to be careful about how quickly the DMP trajectory moves, because while the DMP system isn’t constrained by any physical dynamics, the plant is. Depending on the size of the movement the DMP trajectory may be moving a foot a second or an inch a second. You can see above that the arm doesn’t fully draw out the desired trajectories in places where the DMP system moved too quickly in and out and sharp corners. The only way to remedy this without feedback is to have the DMP system move more slowly throughout the entire trajectory. What would be nice, instead, would be to just say ‘go as fast as you can, as long as the plant state is within some threshold distance of you’, and this is where system feedback comes in.

It’s actually very straightforward to implement this using system feedback: If the plant state drifts away from the state of the DMPs, slow down the execution speed of the DMP to allow the plant time to catch up. The do this we just have to multiply the DMP timestep by a new term:

.

All this new term does is slow down the canonical system when there’s an error, you can think of it as a scaling on the time step. Additionally, the sensitivity of this term can be modulated the scaling term on the difference between the plant and DMP states.

We can get an idea of how this affects the system by looking at the dynamics of the canonical system when an error term is introduced mid-run:

When the error is introduced the dynamics of the system slow down, great! Lets look at an example comparing execution with and without this feedback term. Here’s the system drawing the number 3 without any feedback incorporation:

and here’s the system drawing the number 3 with the feedback term included:

These two examples are a pretty good case for including the feedback term into your DMP system. You can still see in the second case that the specified trajectory isn’t traced out exactly, but if that’s what you’re shooting for you can just crank up the to make the DMP timestep really slow down whenever the DMP gets ahead of the plant at all.

Interpolating trajectories for imitation

When imitating trajectories there can be some issues with having enough sample points and how to fit them to the canonical system’s timeframe, they’re not difficult to get around but I thought I would go over what I did here. The approach I took was to always run the canonical system for 1 second, and whenever a trajectory is passed in that should be imitated to scale the x-axis of the trajectory such that it’s between 0 and 1. Then I shove it into an interpolator and use the resulting function to generate an abundance of nicely spaced sample points for the DMP imitator to match. Here’s the code for that:

# generate function to interpolate the desired trajectory
import scipy.interpolate

path = np.zeros((self.dmps, self.timesteps))
x = np.linspace(0, self.cs.run_time, y_des.shape[1])

for d in range(self.dmps):

# create interpolation function
path_gen = scipy.interpolate.interp1d(x, y_des[d])

# create evenly spaced sample points of desired trajectory
for t in range(self.timesteps):
path[d, t] = path_gen(t * self.dt)

y_des = path

Direct trajectory control vs DMP based control

Now, using the above described interpolation function we can just directly use its output to guide our system. And, in fact, when we do this we get very precise control of the end-effector, more precise than the DMP control, as it happens. The reason for this is because our DMP system is approximating the desired trajectory and with a set of basis functions, and some accuracy is being lost in this approximation.

So if we instead use the interpolation function to drive the plant we can get exactly the points that we specified. The times when this comes up especially are when the trajectories that you’re trying to imitate are especially complicated. There are ways to address this with DMPs by placing your basis functions more appropriately, but if you’re just looking for the exact replication of an input trajectory (as often people are) this is a simpler way to go. You can see the execution of this in the trace.py code up on my github. Here’s a comparison of a single word drawn using the interpolation function:

and here’s the same word drawn using a DMP system with 1,000 basis function per DOF:

We can see that just using the interpolation function here gives us the exact path that we specified, where using DMPs we have some error, and this error increases with the size of the desired trajectory. But! That’s for exactly following a given trajectory, which is often not the case. The strength of the DMP framework is that the trajectory is a dynamical system. This lets us do simple things to get really neat performance, like scale the trajectory spatially on the fly simply by changing the goal, rather than rescaling the entire trajectory:

Conclusions

Some basic examples of using DMPs to control the end-effector trajectory of an arm with operational space control were gone over here, and you can see that they work really nicely together. I like when things build like this. We also saw that power of DMPs in this situation is in their generalizability, and not in exact reproduction of a given path. If I have a single complex trajectory that I only want the end-effector to follow once then I’m going to be better off just interpolating that trajectory and feeding the coordinates into the arm controller rather than go through the whole process of setting up the DMPs.

Drawing words, though, is just one basic example of using the DMP framework. It’s a very simple application and really doesn’t do justice to the flexibility and power of DMPs. Other example applications include things like playing ping pong. This is done by creating a desired trajectory showing the robot how to swing a ping pong paddle, and then using a vision system to track the current location of the incoming ping pong ball and changing the target of the movement to compensate dynamically. There’s also some really awesome stuff with object avoidance, that is implemented by adding another term with some simple dynamics to the DMP. Discussed here, basically you just have another system that moves you away from the object with a strength relative to your distance from the object. You can also use DMPs to control gain terms on your PD control signal, which is useful for things like object manipulation.

And of course I haven’t touched on rhythmic DMPs or learning with DMPs at all, and those are both also really interesting topics! But this serves as a decent introduction to the whole area, which has been developed in the Schaal lab over the last decade or so. I recommend further reading with some of these papers if you’re interested, there are a ton of neat ways to apply the DMP framework! And, again, the code for everything here is up on my github in the control and pydmps repositories.

Robot control part 7: OSC of a 3-link arm

So we’ve done control for the 2-link arm, and control of the one link arm is trivial (where we control joint angle, or x or y coordinate of the pendulum), so here I’ll just show an implementation of operation space control for a more interesting arm model, the 3-link arm model. The code can all be found up on my Github.

In theory there’s nothing different or more difficult about controlling a 3-link arm versus a 2-link arm. For the inertia matrix, what I ended up doing here is just jacking up all the values of the matrix to about 100, which causes the controller to way over control the arm, and you can see the torques are much larger than they would need to be if we had an accurate inertia matrix. But the result is the same super straight trajectories that we’ve come to expect from operational space control:

It’s a little choppy because I cut out a bunch of frames to keep the gif size down. But you get the point, it works. And quite well!

Because this is also a 3-link arm now and our task space force signal is 2D, we have redundant space of solutions, meaning that the task space control signal can be carried out in a number of ways. In other words, a null space exists for this controller. This means that we can throw another controller in our system to operate inside the null space of the first controller. We’ve already worked through all the math for this, so it’s straightforward to implement.

What kind of null space controller should we put in? Well, you may have noticed in the above animation the arm goes through itself, here’s another example:

Often it’s desirable to avoid this (because of physics or whatever), so what we can do is add a secondary controller that works to keep the arm’s elbow and wrist near some comfortable default angles. When we do this we get the following:

And there you have it! Operational space control of a three link arm with a secondary controller in the null space to try to keep the angles near their default / resting positions.

I also added mouse based control to the arm so it will try to follow your mouse when you move over the figure, which makes it pretty fun to explore the power of the controller. It’s interesting to see where the singularities become an issue, and how having a null space controller that’s operating in joint space can actually come to help the system move through those problem points more smoothly. Check it out! It’s all up on my Github.

Robot control part 6: Handling singularities

We’re back! Another exciting post about robotic control theory, but don’t worry, it’s short and ends with simulation code. The subject of today’s post is handling singularities.

What is a singularity

This came up recently when I had build this beautiful controller for a simple two link arm that would occasionally go nuts. After looking at it for a while it became obvious this was happening whenever the elbow angle reached or got close to 0 or . Here’s an animation:

What’s going on here? Here’s what. The Jacobian has dropped rank and become singular (i.e. non-invertible), and when we try to calculate our mass matrix for operational space

the values explode in the inverse calculation. Dropping rank means that the rows of the Jacobian are no longer linearly independent, which means that the matrix can be rotated such that it gives a matrix with a row of zeros. This row of zeros is the degenerate direction, and the problems come from trying to send forces in that direction.

To determine when the Jacobian becomes singular its determinant can be examined; if the determinant of the matrix is zero, then it is singular. Looking the Jacobian for the end-effector:

When it can be that , so the Jacobian becomes

which gives a determinant of

Similarly, when , where and , the Jacobian is

Calculating the determinant of this we get

Note that while in these cases the Jacobian is a square matrix in the event that it is not a square matrix, the determinant of can be found instead.

Fixing the problem

When a singularity is occurring it can be detected, but now it must be handled such that the controller behaves appropriately. This can be done by identifying the degenerate dimensions and setting the force in those directions to zero.

First the SVD decomposition of is found. To get the inverse of this matrix (i.e. to find ) from the returned and matrices is a matter of inverting the matrix :

where is a diagonal matrix of singular values.

Because is diagonal it is very easy to find its inverse, which is calculated by taking the reciprocal of each of the diagonal elements.

Whenever the system approaches a singularity some of the values of will start to get very small, and when we take the reciprocal of them we start getting huge numbers, which is where the value explosion comes from. Instead of allowing this to happen, a check for approaching the singularity can be implemented, which then sets the singular values entries smaller than the threshold equal to zero, canceling out any forces that would be sent in that direction.

Here’s the code:

Mx_inv = np.dot(JEE, np.dot(np.linalg.inv(Mq), JEE.T))
if abs(np.linalg.det(np.dot(JEE,JEE.T))) > .005**2:
    # if we're not near a singularity
    Mx = np.linalg.inv(Mx_inv)
else:
    # in the case that the robot is entering near singularity
    u,s,v = np.linalg.svd(Mx_inv)
    for i in range(len(s)):
        if s[i] < .005: s[i] = 0
        else: s[i] = 1.0/float(s[i])
    Mx = np.dot(v, np.dot(np.diag(s), u.T))

And here’s an animation of the controlled arm now that we’ve accounted for movement when near singular configurations:

As always, the code for this can be found up on my Github. The default is to run using a two link arm simulator written in Python. To run, simply download everything and run the run_this.py file.

Everything is also included required to run the MapleSim arm simulator. To do this, go into the TwoLinkArm folder, and run python setup.py build_ext -i. This should compile the arm simulation to a shared object library that Python can now access on your system. To use it, edit the run_this.py file to import from TwoLinkArm/arm_python to TwoLinkArm/arm and you should be good to go!
More details on getting the MapleSim arm to run can be found in this post.

Robot control part 5: Controlling in the null space

In the last post, I went through how to build an operational space controller. It was surprisingly easy after we’ve worked through all the other posts. But maybe that was a little too easy for you. Maybe you want to do something more interesting like implement more than one controller at the same time. In this post we’ll go through how to work inside the null space of a controller to implement several seperate controllers simultaneously without interference.
Buckle up.

Null space forces

The last example comprises the basics of operational space control; describe the system, calculate the system dynamics, transform desired forces from an operational space to the generalized coordinates, and build the control signal to cancel out the undesired system dynamics. Basic operational space control works quite well, but it is not uncommon to have several control goals at once; such as `move the end-effector to this position’ (primary goal), and `keep the elbow raised high’ (secondary goal) in the control of a robot arm.

If the operational space can also serve as generalized coordinates, i.e. if the system state specified in operational space constrains all of the degrees of freedom of the robot, then there is nothing that can be done without affecting the performance of the primary controller. In the case of controlling a two-link robot arm this is the case. The end-effector Cartesian space (chosen as the operational space) could also be a generalized coordinates system, because a specific position fully constrains the position of the arm.

But often when using operational space control for more complex robots this is not the case. In these situations, the forces controlled in operational space have fewer dimensions than the robot has degrees of freedom, and so it is possible to accomplish the primary goal in a number of ways. The null space of this primary controller is the region of state space where there is a redundancy of solutions; the system can move in a number of ways and still not affect the completion of the goals of the primary controller. An example of this is all the different configurations the elbow can be in while a person moves their hand in a straight line. In these situations, a secondary controller can be created to operate in the null space of the primary controller, and the full control signal sent to the system is a sum of the primary control signal and a filtered version of the secondary control signal. In this section the derivation of the null-space filter will be worked through for a system with only a primary and secondary controller, but note that the process can be applied iteratively for systems with further controllers.

The filtering of the secondary control signal means that the secondary controller’s goals will only be accomplished if it is possible to do so without affecting the performance of the first controller. In other words, the secondary controller must operate in the null space of the first controller. Denote the primary operational space control signal, e.g. the control signal defined in the previous post, as and the control signal from the secondary controller . Define the force to apply to the system

where is the pseudo-inverse of .

Examining the filtering term that was added,

it can be seen that the Jacobian transpose multiplied by its pseudo-inverse will be 1’s all along the diagonal, except in the null space. This means that is subtracted from itself everywhere that affects the operational space movement and is left to apply any arbitrary control signal in the null space of the primary controller.

Unfortunately, this initial set up does not adequately filter out the effects of forces that might be generated by the secondary controller. The Jacobian is defined as a relationship between the velocities of two spaces, and so operating in the null space defined by the Jacobian ensures that no velocities are applied in operational space, but the required filter must also prevent any accelerations from affecting movement in operational space. The standard Jacobian pseudo-inverse null space is a velocity null space, and so a filter built using it will allow forces affecting the system’s acceleration to still get through. What is required is a pseudo-inverse Jacobian defined to filter signals through an acceleration null space.

To acquire this acceleration filter, our control signal will be substituted into the equation for acceleration in the operational space, which, after cancelling out gravity effects with the control signal and removing the unmodeled dynamics, gives

Rewriting this to separate the secondary controller into its own term

it becomes clear that to not cause any unwanted movement in operational space the second term must be zero.

There is only one free term left in the second term, and that is the pseudo-inverse. There are numerous different pseudo-inverses that can be chosen for a given situation, and here what is required is to engineer a pseudo-inverse such that the term multiplying in the above operational space acceleration equation is guaranteed to go to zero.

this needs to be true for all , so it can be removed,

substituting in our inertia matrix for operational space, which defines

This specific Jacobian inverse was presented in this 1987 paper by Dr. Oussama Khatib and is called the `dynamically consistent generalized inverse’. Using this psuedo-inverse guarantees that any signal coming from the secondary controller will not affect movement in the primary controller’s operational space. Just as a side-note, the name ‘pseudo-inverse’ is a bit of misnomer here, since it doesn’t try to produce the identity when multiplied by the original Jacobian transpose, but hey. That’s what they’re calling it.

The null space filter cancels out the acceleration effects of forces in operational space from a signal that is being applied as part of the control system. But it can also be used to cancel out the effects of any unwanted signal that can be modeled. Given some undesirable force signal interfering with the system that can be effectively modeled, a null space filtering term can be implemented to cancel it out. The control signal in this case, with one primary operational space controller and a null space filter for the undesired force, looks like:

We did it! This will now allow a high-priority operational space controller to execute without interference from a secondary controller operating in its null space to complete it’s own set of goals (when possible).

Example:

Given a three link arm (revolute-revolute-revolute) operating in the plane, shown below:

this example will construct the control system for a primary controller controlling the end-effector and a secondary controller working to keep the arm near its joint angles’ default resting positions.

Let the system state be  with default positions . The control signal of the secondary controller is the difference between the target state and the current system state

where is a gain term.

Let the centres of mass be

the Jacobians for the COMs are

The Jacobian for the end-effector of this three link arm is

where and .

Taking the control signal developed in Section~\ref{sec:exampleOS}

where was defined in the previous post, and is defined two posts ago, and and are gain terms, usually set such that , and adding in the null space control signal and filter gives

where is the dynamically consistent generalized inverse defined above, and is our null space signal!

Conclusions

It’s a lot of math, but when you start to get a feel for it what’s really awesome is that this is it. We’re describing the whole system, and so by working with these equations we can get a super effective controller. Which is pretty cool. Especially in relation to other possible controllers.

Alright! We’ve now worked through all the basic theory for operational space control, it is time to get some implementations going.

Robot control part 4: Operation space control

In this post we’ll look at operational space control and how to derive the control equations. I’d like to mention again that these posts have all come about as a result of me reading and working through Samir Menon’s operational space control tutorial, where he works through an implementation example on a revolute-prismatic-prismatic robot arm.

Generalized coordinates vs operational space

The term generalized coordinates refers to a characterization of the system that uniquely defines its configuration. For example, if our robot has 7 degrees of freedom, then there are 7 state variables, such that when all these variables are given we can fully account for the position of the robot. In the previous posts of this series we’ve been describing robotic arms in joint space, and for these systems joint space is an example of generalized coordinates. This means that if we know the angles of all of the joints, we can draw out exactly what position that robot is in. An example of a coordinate system that does not uniquely define the configuration of a robotic arm would be one that describes only the position of the end-effector.

So generalized coordinates tell us everything we need to know about where the robot is, that’s great. The problem with generalized coordinates, though, is that planning trajectories in this space for tasks that we’re interested in performing tends not to be straight forward. For example, if we have a robotic arm, and we want to control the position of the end-effector, it’s not obvious how to control the position of the end-effector by specifying a trajectory for each of the arm’s joints to follow through joint space.

The idea behind operational space control is to abstract away from the generalized coordinates of the system and plan a trajectory in a coordinate system that is directly relevant to the task that we wish to perform. Going back to the common end-effector position control situation, we would like to operate our arm in 3D Cartesian space. In this space, it’s obvious what trajectory to follow to move the end-effector between two positions (most of the time it will just be a straight line in each dimension). So our goal is to build a control system that lets us specify a trajectory in our task space and will transform this signal into generalized coordinates that it can then send out to the system for execution.

Operational space control of simple robot arm

Alright, we’re going to work through an example. The generalized coordinates for this example is going to be joint space, and the operational space is going to be the end-effector Cartesian coordinates relative to the a reference frame attached to the base. Recycling the robot from the second post in this series, here’s the set up we’ll be working with:

Once again, we’re going to need to find the Jacobians for the end-effector of the robot. Fortunately, we’ve already done this:

Great! So now that we have , we can go ahead and transform forces from end-effector (hand) space to joint space as we discussed in the second post:

Rewriting as its component parts

where is end-effector acceleration, and is the inertia matrix in operational space. Unfortunately, this isn’t just the normal inertia matrix, so let’s take a look here at how to go about deriving it.

Inertia in operational space

Being able to calculate allows inertia to be cancelled out in joint-space by incorporating it into the control signal, but to cancel out the inertia of the system in operational space more work is still required. The first step will be calculating the acceleration in operational space. This can be found by taking the time derivative of our original Jacobian equation.

Substituting in the dynamics of the system, as defined in the previous post, but ignoring the effects of gravity for now, gives:

Define the control signal

where substituting in for , the desired end-effector force, gives

where denotes the desired end-effector acceleration. Substituting the above equation into our equation for acceleration in operational space gives

Rearranging terms leads to

the last term is ignored due to the complexity of modeling it, resulting in

At this point, to get the dynamics to be equal to the desired acceleration , the end-effector inertia matrix needs to be chosen carefully. By setting

we now get

And that’s why and how the inertia matrix in operational space is defined!

The whole signal

Going back to the control signal we were building, let’s now add in a term to cancel the effects of gravity in joint space. This gives

where is the same as defined in the previous post. This controller converts desired end-effector acceleration into torque commands, and compensates for inertia and gravity.

Defining a basic PD controller in operational space

and the full equation for the operational space control signal in joint space is:

Hurray! That was relatively simple. The great thing about this, though, is that it’s the same process for any robot arm! So go out there and start building controllers! Find your robot’s mass matrix and gravity term in generalized coordinates, the Jacobian for the end effector, and you’re in business.

Conclusions

So, this feels a little anticlimactic without an actual simulation / implementation of operational space, but don’t worry! As avid readers (haha) will remember, a while back I worked out how to import some very realistic MapleSim arm simulations into Python for use with some Python controllers. This seems a perfect application opportunity, so that’s next! A good chance to work through writing the controllers for different arms and also a chance to play with controllers operating in null spaces and all the like.

Actual simulation implementations will also be a good chance to play with trying to incorporate those other force terms into the control equation, and get to see the results without worrying about breaking an actual robot. In actual robots a lot of the time you leave out anything where your model might be inaccurate because the last thing to do is falsely compensate for some forces and end up injecting energy into your system, making it unstable.

There’s still some more theory to work through though, so I’d like to do that before I get to implementing simulations. One more theory post, and then we’ll get back to code!