Velocity limiting in operational space control

Recently, I was reading through an older paper on effective operational space control, talking specifically point to point control in operational space. The paper mentioned that even if you have a perfect model of the system, you’re going to run into trouble if you use just a basic PD formula to define your control signal in operational space:

where and are the system position and velocity in operational space, is the target position, and and are gains.

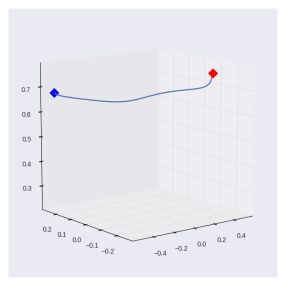
If you define your operational space control signal like this, and then translate this signal into joint torques (using, for example, methods discussed in other posts), you’re going to see a very non-straight trajectory emerge in larger movements as a result of “actuator saturation, and bandwidth and velocity limitations”. In the example of a standard robot, you might run into issues with your motors not being able to actually generate the torques that have been specified, the frequency of control and feedback might not be sufficient, and you could hit hard constraints on system velocity. The solution to this problem was presented in this 1987 paper by Dr. Oussama Khatib, and is pretty slick and very useful, so I thought I’d write it up here for any other unfortunate souls wandering around in ignorance. First though, here’s what it looks like to move large point to point distances without velocity limiting:

As you can see, the system isn’t moving in a straight line, which can be very aggravating if you’ve worked and reworked out the equations and double checked all your parameters, etc etc. A few things, first, when working with simulations it’s easy to forget how ridiculously fast this actually would be in real-time. Even though it takes a minute to simulate the above movement, in real-time, is happening over the course of 200ms. Taking that into account, this is pretty good. Also, there’s an obvious solution here, slow down your movement. The source of this problem is largely that all of the motors are not able to apply the torques specified and move at the required speed. Some of the motors have a lot less mass to throw around and will be able to move at the specified torques, but not all. Hence the not straight trajectory.

You can of course drop the gains on your PD signal, but that’s not really a great methodical solution. So, what can we do?

Well, if we rearrange the PD control signal specified above into

where is the desired velocity, we see that this signal can be interpreted as a pure velocity servo-control signal, with velocity gain and a desired velocity

.

When things are in this form, it becomes a bit more clear what we have to do: limit the desired velocity to be at most some specified maximum velocity of the end-effector, . This value should be low enough that the transformation into joint torques doesn’t result in anything larger than the actuators can generate.

Taking , what we want is to clip the magnitude of the control signal to be if it’s ever larger (in positive or negative directions), and to be equal to otherwise. The math for this works out such that we can accomplish this with a control signal of the form:

,

where , , and is the saturation function, such that

where is the absolute value of , and is applied element wise to the vector in the control signal.

As a result of using this saturation function, the control signal behaves differently depending on whether or not :

where is a function that returns -1 if and 1 if , and is again applied element-wise to vectors. Note that the control signal in the second condition is equivalent to our original PD control signal . If you’re wondering about negative signs make sure you note that and not , as you might assume.

So now the control signal is behaving exactly as desired! Moves the system towards the target, but no faster than the specified maximum velocity. Now our trajectories look like this:

So those are starting to look a lot better! The first thing you’ll notice is that this is a fair bit slower of a movement. Well, actually, it’s waaaayyyy slower because the playback speed here is 4x faster than in that first animation, and this is a movement over 2s. Which has pros and cons, con: it’s slower, pro: it’s straighter, and you’re less likely to be murdered by it. When you move from simulations to real systems that latter point really moves way up the priority list.

Second thing to notice, the system seems to be minimising the error along one dimension, and then along the next, and then arrives at the target. What’s going on?  Because the error along each of the dimensions isn’t the same, when speed gets clipped along one of the dimensions you’re no longer going to be moving in a straight line directly to the target. To address this, we’re going to add a scaling term whenever clipping happens, such that you reduce the speed you move along each dimension by the same ratio, so that you’re still moving in a straight line.

It’s a liiiiittle bit more complicated than that, but not much. First, we’ll calculate the values being passed in to the saturation function for each dimension. We’ll then check to see if any of them are going to get clipped, and if there’s more than one that saturates we’ll find the one that is affected the most. After we’ve identified which dimension it is, we go through and calculate what the control signal would have been without velocity limiting, and what it will be now with velocity limiting. This scaling term tells us how much the control signal was reduced, and we can then use it to reduce the control signals of the other dimensions by the same amount. These other dimensions might still saturate, though, so we have to recalculate the saturation function for them once they’ve been scaled. Here’s what this all looks like in code:

# implement velocity limiting
lamb = kp / kv
x_tilde = xyz - target_xyz
sat = vmax / (lamb * np.abs(x_tilde))
scale = np.ones(3)
if np.any(sat < 1):
    index = np.argmin(sat)
    unclipped = kp * x_tilde[index]
    clipped = kv * vmax * np.sign(x_tilde[index])
    scale = np.ones(3) * clipped / unclipped
    scale[index] = 1
u_xyz = -kv * (dx + np.clip(sat / scale, 0, 1) *
               scale * lamb * x_tilde)
 

And now, finally, we start getting the trajectories that we’ve been wanting the whole time:

And finally we can rest easy, knowing that our robot is moving at a reasonable speed along a direct path to its goals. Wherever you’d like to use this neato ‘ish you should be able to just paste in the above code, define your vmax, kp, and kv values and be good to go!